All Trigonometry Formulae || Complete List of Trigonometry Formulae

Dear readers, in this article I provide all Trigonometry Formulae for all students, aspirants for competitive examination. You can read also an important List of Chemical Names and formulas: All common Formulas for all competitive examinations like Railway, SSC, Banking, IAS, State PSU, etc.

All Basic Trigonometry Formulae are:- 

In a Right-angled Triangle,

Hypotenuse-h

Perpendicular-p

Base-b

Hypotenuse: The longest side of the triangle which in front of the right angle(90⁰).

Perpendicular: The side making an angle of 90 degrees with the Base.

Base: The side that is horizontal to the plane.

Trigonometry Formulae: Pythagoras Theorem

In ABC Δ  ,AB² + BC² = AC²

h² = p² + b²

h = √p² + b²

p² = h² – b²

p = √h² – b²

b² = h² -p² 

b = √h² -p² 

There are basically 6 Ratios in Trigonometry to find the elements in Trigonometry:-sine, cosine, tangent, cotangent, secant, cosecant. Generally, we read as Sin, cos, tan, cot, sec, and cosec.

Relations among trigonometrial ratios

• sin θ =  Perpendicular /Hypotenuse =p/h
• cos θ = Base /Hypotenuse =b/h
• tan θ  = Perpendicular/ Base =p/b
• cot θ =  Base /Perpendicular = b/p
• sec θ = Hypotenuse/ Base =h/b
• cosec θ = Hypotenuse/ Perpendicular =h/p

Sine and Cosine Law Trigonometry Formulae

The Sine and Cosine Law gives a relationship between the sides and angles of a triangle.  

Sine Law:-

The Sine Law gives the ratio of the sides and the angle opposite to the side.  The ratio is taken for the side ‘a’ and its opposite angle ‘A’.

   

 

 

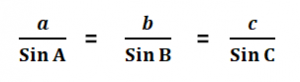
Cosine Law:-

The Cosine Law helps to find the length of a side, for the given lengths of the other two sides and the included angle.  

The length ‘a’ can be found with the help of the other two sides ‘b’ and ‘c’ and their included angle ‘A’.

• a²=b²+c²−2bc Cos A,
• b²=a²+c²−2ac Cos B,
• c²=a²+b²−2ab Cos C.

Reciprocal Relations:

 

 

 

 

 

 

 

 

 

 

 

 

Square Relations in Trigonometry Formulae:

• sin² θ + cos² θ = 1
• sec² θ – tan² θ = 1
• cosec² θ – cot² θ = 1
• sin² θ= 1- cos² θ
• cos² θ = 1 – sin² θ
• sec² θ = 1 + tan² θ
• tan² θ = sec² θ -1
• cosec² θ = 1 + cot² θ
• cot² θ = cosec² θ -1

Quotient Relations in Trigonometry Formulae:

 

 

 

 

 

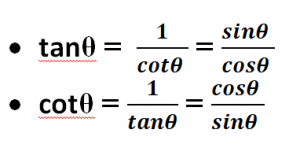
Trigonometric Functions Of Sum And Difference Of Two Angles

Trigonometrical ratios of compound angles

1. sin (A+B)= sin A. cos B + cos A. sin B
2. sin (A−B)= sin A. cos B – cos A. sin B
3. cos (A+B)= cos A.cos B – sin A. sin B
4. cos (A−B)= cos A.cos B + sin A. sin B

 

 

 

 

 

 

 

 

 

• sin (A + B) + sin (A – B) = 2 sin A . cos B
• sin (A + B) – sin (A – B) = 2 cos A . sin B
• cos (A + B) + cos (A – B) = 2 cos A . cos B
• cos (A – B) – cos (A + B) = 2 sin A . sin B

 

• sin (A + B) . sin (A – B) = sin² A – sin² B = cos² B – cos² A
• cos (A + B) . cos (A – B) = cos² A – sin² B = cos² B – sin² A

Sum to Product Identities

 

 

 

 

 

 

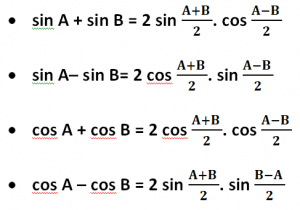
Product identities

 

 

 

 

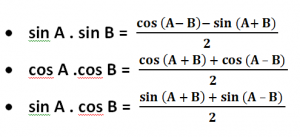
Double Angle Formulas

1. Sin 2A = 2 sin A .cos A = tan A/1+ tan² A
2. Cos 2A = cos² A − sin² A

• Cos 2A = = 2 cos² θ − 1
• Cos 2A = = 1 − 2 sin² θ

3. tan 2A= 2 tan A /1 − tan² A
4. cot 2A=cot²A-1/2cotA

• 1 + Sin 2A = (cosA + sinA)²
• 1 – Sin 2A = (cosA – sinA)²
• 1+cos 2A= 2cos²A
• 1-cos 2A= 2sin²A

Half Angle Formula in Trigonometry 

 

 

 

 

 

 

 

 

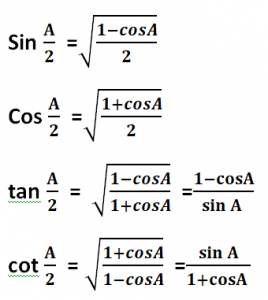
Co-function Identities (in Degrees) (0⁰  < θ < 90⁰)

• sin (90⁰ – θ )= cos θ
• cos (90⁰ – θ )= sin θ
• tan (90⁰ – θ ) = cot θ
• cot (90⁰ – θ ) = tan θ
• sec (90⁰ – θ )= cosec θ
• cosec (90⁰ – θ ) = sec θ

90⁰  < θ < 180⁰

• sin (90⁰ +θ ) = cos θ
• cos (90⁰ +θ )= – sin θ
• tan (90⁰ +θ ) = –cot θ
• cot (90⁰ +θ ) = –tan θ
• sec (90⁰ +θ )= -cosec θ
• cosec (90⁰ + θ ) = sec θ

0⁰ < θ < 180⁰

sin (180⁰-θ )= sin θ

cos (180⁰-θ )=- cos θ

tan (180⁰-θ ) = – tan θ

cot (180⁰-θ ) = – cot θ

sec (180⁰-θ )= – sec θ

cosec (180⁰– θ ) = cosec θ

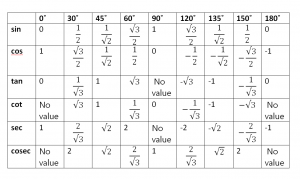
Trigonometric Table Value